The process of finding an alternate location is called collision resolution.
- Direct Chaining: An array of linked list application
- Separate chaining
- Open Addressing: Array-based implementation
- Linear probing (linear search)
- Quadratic probing (nonlinear search)
- Double hashing (use two hash functions)
Separate Chaining : See Program
When a collision occurs, elements with the same hash key will be chained together. A chain is simply a linked list of all the elements with the same hash key.
Linear Probing
When using a linear probe, the item will be stored in the next available slot in the table, assuming that the table is not already full.
If an empty slot is not found before reaching the point of collision, the table is full.
One of the problems with linear probing is that table items tend to cluster together in the hash table. This means that the table contains groups of consecutively occupied locations that are called clustering. Clusters can get close to one another, and merge into a larger cluster. Thus, the one part of the table might be quite dense, even though another part has relatively few items. Clustering causes long probe searches and therefore decreases the overall efficiency.
Quadratic Probing
To resolve the primary clustering problem, quadratic probing can be used. With quadratic probing, rather than always moving one spot, move i2 spots from the point of collision, where i is the number of attempts to resolve the collision.
Limitation: at most half of the table can be used as alternative locations to resolve collisions.
This means that once the table is more than half full, it's difficult to find an empty spot. This new problem is known as secondary clustering because elements that hash to the same hash key will always probe the same alternative cells.
Double hashing uses the idea of applying a second hash function to the key when a collision occurs.
The second hash function h2 should be:
We first probe the location h1( key).
If the location is occupied, we probe the location h1( key) + h2( key), h1( key) + 2 * h2( key), ...
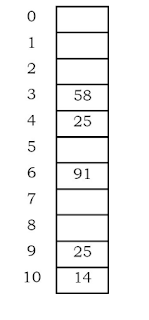
Example:
Table size is 11 (0.. 10)
Hash Function: assume h1( key) = key mod 11 and h2( key) = 7- (key mod 7)
This means that once the table is more than half full, it's difficult to find an empty spot. This new problem is known as secondary clustering because elements that hash to the same hash key will always probe the same alternative cells.
Double Hashing
Double hashing uses the idea of applying a second hash function to the key when a collision occurs.The second hash function h2 should be:
We first probe the location h1( key).
If the location is occupied, we probe the location h1( key) + h2( key), h1( key) + 2 * h2( key), ...
Example:
Table size is 11 (0.. 10)
Hash Function: assume h1( key) = key mod 11 and h2( key) = 7- (key mod 7)










No comments:
Post a Comment