Graph

A graph is a pair (V, E), where V is a set of nodes, called vertices, and E is a collection of pairs of vertices, called edges.

• Directed Edge: Example - One way road traffic

• Undirected Edge: Example - Railway lines

• Directed Graph: Example - Route Network

• Undirected Graph: Example - Flight Network

When an edge connects two vertices, the vertices are said to be adjacent to each other and the edge is incident on both vertices.


A graph with no cycles is called a tree. A tree is an acyclic connected graph.

A self loop is an edge that connects a vertex to itself.

Two edges are parallel if they connect the same pair of vertices.

The Degree of a vertex is the number of edges incident on it.

A path in a graph is a sequence of adjacent vertices. Simple path is a path with no repeated vertices. In the graph below, the dotted lines represent a path from G to E.

A graph is connected if there is a path from every vertex to every other vertex.
If a graph is not connected then it consists of a set of connected components.

A directed acyclic graph [DAG] is a directed graph with no cycles.

A forest is a disjoint set of trees. 

A spanning tree of a connected graph is a subgraph that contains all of that graph’s vertices and is a single tree. A spanning forest of a graph is the union of spanning trees of its connected components. 

A bipartite graph is a graph whose vertices can be divided into two sets such that all edges connect a vertex in one set with a vertex in the other set.

In weighted graphs integers (weights) are assigned to each edge to represent (distances or costs).

Graphs with all edges present are called complete graphs.

Graphs with relatively few edges (generally if it edges < | V | log | V |) are called sparse graphs. 

Graphs with relatively few of the possible edges missing are called dense.

Directed weighted graphs are sometimes called network. 

We will denote the number of vertices in a given graph by | V |, and the number of edges by | E |. 

Note that E can range anywhere from 0 to | V |( | V | – l)/ 2 (in undirected graph). This is because each node can connect to every other node.

Graph Representation

• Adjacency Matrix 
• Adjacency List 
• Adjacency Set

Topological Sort

Topological sort is an ordering of vertices in a directed acyclic graph [DAG] in which each node comes before all nodes to which it has outgoing edges. 

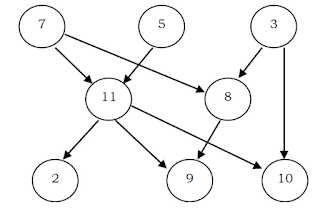
Example: If we have to install packages. Suppose package C has to be installed after A and B and D has dependency on C package , so we will create a DAG as below:

We start with nodes which do not have any prerequisite like, 7, 5 and 3 in the below case:

7, 5, 3, 11, 8, 2, 9, 10 and 3, 5, 7, 8, 11, 2, 9, 10 are both topological orderings.

Initially, indegree is computed for all vertices, starting with the vertices which are having indegree 0. That means consider the vertices which do not have any prerequisite.

Applications of Topological Sorting 

• Representing course prerequisites 
• Detecting deadlocks 
• Pipeline of computing jobs 
• Checking for symbolic link loop 
• Evaluating formulae in spreadsheet

Algorithm: Program

• Take a bool array visited and set all to false
• Declare int stack
• starting with i = 0 check if its not visited
• Call recursive function
•  make visited[i] = true
• take the temp as arr[i].head
• Loop through all the nodes of i till temp is not NULL and its not visited already
• Call recursive function for the data of next node
• temp = temp->next
• Call will come to this part when the last node which don't have any dependency or link, we push it into Stack.
•  Pop the element from stack and print the topological sort

Shortest Path Algorithms