Greedy Algorithms

Example: Game of chess - when we play a move, we have to also think about the future consequences. Whereas, in the game of Tennis (or Volleyball), our action is based on the immediate situation.

The Greedy technique is best suited for looking at the immediate situation.

Greedy Strategy

Greedy algorithms work in stages. In each stage, a decision is made that is good at that point, without bothering about the future. This means that some local best is chosen. It assumes that a local good selection makes for a global optimal solution.

Two basic properties of optimal Greedy algorithms

Greedy choice property

• This property says that the globally optimal solution can be obtained by making a locally optimal solution

Optimal substructure 

• A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the subproblems. That means we can solve subproblems and build up the solutions to solve larger problems.

Note: Making locally optimal choices does not always work.

Advantage: 

We do not have to spend time re-examining the already computed values, once decision is made.

Disadvantage: 

In many cases there is no guarantee that making locally optimal improvements in a locally optimal solution gives the optimal global solution.

Greedy Applications 

• Sorting: Selection sort, Topological sort 
• Priority Queues: Heap sort 
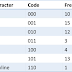
• Huffman coding compression algorithm 
• Prim’s and Kruskal’s algorithms 
• Shortest path in Weighted Graph [Dijkstra’s] 
• Coin change problem 
• Fractional Knapsack problem 
• Disjoint sets-UNION by size and UNION by height (or rank) 
• Job scheduling algorithm 
• Greedy techniques can be used as an approximation algorithm for complex problems